(本小题满分14分)
已知函数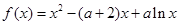 ,其中常数
,其中常数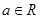 .
.
(Ⅰ)当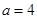 时,求函数
时,求函数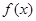 的极值点;
的极值点;
(Ⅱ)令 ,若函数
,若函数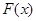 在区间
在区间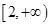 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅲ)设定义在D上的函数 在点
在点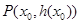 处的切线方程为
处的切线方程为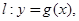 当
当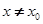 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“特殊点”,请你探究当
的“特殊点”,请你探究当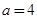 时,函数
时,函数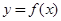 是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
直线l经过P(2,3),且在x,y轴上的截距相等,试求该直线方程.
已知正方形ABCD 对角线AC所在直线方程为 .抛物线
.抛物线 过B,D两点
过B,D两点
(1)若正方形中心M为(2,2)时,求点N(b,c)的轨迹方程。
(2)求证方程 的两实根
的两实根 ,
, 满足
满足
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件|F2A|、|F2B|、|F2C|成等差数列(1)求该弦椭圆的方程;(2)求弦AC中点的横坐标;(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围
如图:在面积为1的DPMN中,tanÐPMN= ,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。