近日,我市多个县区遭遇龙卷风,冰雹等自然灾害,某校八年级两个班各给灾区捐款1800元,已知(2)班比(1)班人均捐款多4元,(2)班的人数比(1)班的人数少10%,请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程。
(本小题满分8分)在直角坐标系中,已知点A(-2,0)、 B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以 D、O、C为顶点的三角形与△AOB相似,求点D的坐标。
B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以 D、O、C为顶点的三角形与△AOB相似,求点D的坐标。
(本小题满分6分)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。
(1)写出图中两对相似三角形(不得添加辅助线);
(2)请分别说明两对三角形相似的理由。
(本小题满分6分)计算:已知二次函数 。
。(1)画出图像,指出对称轴,顶点,求出何时y随x的增大而减小;
(2)写出不等式
 ≥0的解集。
≥0的解集。
.如图,在平面直角坐标系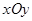 中,点
中,点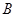 的坐标为
的坐标为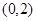 ,点
,点 在
在 轴的正半轴上,
轴的正半轴上, ,
,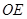 为△
为△ 的中线,过
的中线,过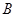 、
、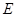 两点的抛物线
两点的抛物线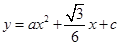 与
与 轴相交于
轴相交于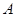 、
、 两点(
两点(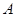 在
在 的左侧).
的左侧).
(1)求抛物线的解析式;
(2)等边△
 的顶点
的顶点 、
、 在线段
在线段 上,求
上,求 及
及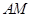 的长;
的长;(3)点
 为△
为△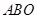 内的一个动点,设
内的一个动点,设 ,请直接写出
,请直接写出 的最小值,以及
的最小值,以及 取得最小值时,线段
取得最小值时,线段 的长.
的长.
.如图,已知抛物线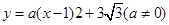 经过点
经过点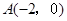 ,抛物线的顶点为
,抛物线的顶点为 ,过
,过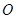 作射线
作射线 .过顶点
.过顶点 平行于
平行于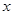 轴的直线交射线
轴的直线交射线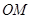 于点
于点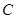 ,
,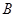 在
在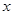 轴正半轴上,连结
轴正半轴上,连结 .
.
(1)求该抛物线的解析式;
(2)若动点
 从点
从点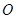 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线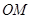 运动,设点
运动,设点 运动的时间为
运动的时间为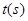 .问当
.问当 为何值时,四边形
为何值时,四边形 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?(3)若
 ,动点
,动点 和动点
和动点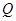 分别从点
分别从点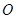 和点
和点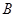 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿 和
和 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
 ,连接
,连接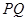 ,当
,当 为何值时,四边形
为何值时,四边形 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时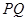 的长.
的长.