(本小题满分16分)
已知函数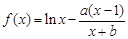 .
.
(1)当 时,若函数
时,若函数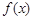 在
在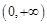 上为单调增函数,求
上为单调增函数,求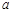 的取值范围;
的取值范围;
(2)当 且
且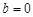 时,求证:函数f (x)存在唯一零点的充要条件是
时,求证:函数f (x)存在唯一零点的充要条件是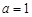 ;
;
(3)设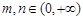 ,且
,且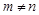 ,求证:
,求证: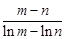 <
<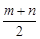 .
.
设函数 ,
,
(1)若不等式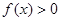 的解集
的解集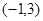 .求
.求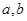 的值;
的值;
(2)若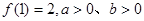 求
求 的最小值.
的最小值.
已知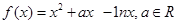 .
.
(1)若a=0时,求函数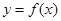 在点(1,
在点(1,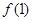 )处的切线方程;
)处的切线方程;
(2)若函数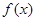 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(3)令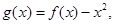 是否存在实数a,当
是否存在实数a,当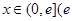 是自然对数的底)时,函数
是自然对数的底)时,函数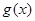 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由.
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴所围成图形的面积;
(3)写出(-∞,+∞)内函数f(x)的单调区间.
设数列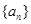 为等差数列,且a3=5,a5=9;数列
为等差数列,且a3=5,a5=9;数列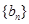 的前n项和为Sn,且Sn+bn=2.
的前n项和为Sn,且Sn+bn=2.
(1)求数列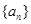 ,
,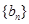 的通项公式;
的通项公式;
(2)若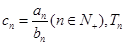 为数列
为数列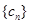 的前n项和,求
的前n项和,求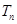 .
.
从集合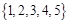 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组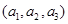 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组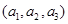 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.