（本小题满分16分）
已知数列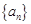
是各项均为正数的等差数列．
（1）若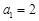
，且
，
，
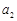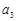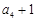成等比数列，求数列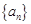的通项公式
；
（2）在（1）的条件下，数列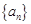的前
和为
，设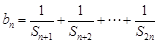
，若对任意的
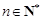，不等式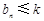
恒成立，求实数
的最小值；
（3）若数列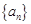中有两项可以表示为某个整数
的不同次幂，求证：数列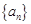 中存在无穷多项构成等比数列．
函数
是R上的偶函数,且当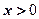
时,函数的解析式为
(1)求
的值;
(2)用定义证明在
上是减函数;
(3)求当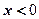
时,函数的解析式;
已知二次函数的图象如图所示．
（1）写出该函数的零点；
（2）写出该函数的解析式．
(3)求当x∈
时，函数的值域.
已知集合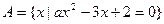
，问
（1）若集合A中至多有一个元素，求
的取值范围；
（2）若集合A中至少有一个元素，求的取值范围。
求下列函数的定义域：
（1）
（2）
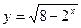
已知A、B、C是直线l上的三点，向量，，满足：
－[y＋2f /(1)]＋ln(x＋1)＝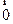
.
（Ⅰ）求函数y＝f(x)的表达式；
（Ⅱ）若x＞0，证明：f(x)＞；
（Ⅲ）若不等式x2≤f(x2)＋m2－2bm－3时，x∈[－1，1]及b∈[－1，1]都恒成立，求实数m的取值范围．