已知A、B、C是直线l上的三点,向量,,满足:
-[y+2f /(1)]+ln(x+1)=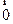 .
.
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>;
(Ⅲ)若不等式x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围.
如图为一个几何体的三视图,主视图和左视图为全等的等腰梯形,上、下底边长分别为 ,
, 。俯视图中内,内外为正方形,边长分别为
。俯视图中内,内外为正方形,边长分别为 ,
, ,几何体的高为
,几何体的高为 ,求此几何体的表面积和体积。(14分)
,求此几何体的表面积和体积。(14分)
若 ,且A∪B=A,求由实数a组成的
,且A∪B=A,求由实数a组成的
集合C.
(本小题满分14分)已知函数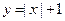 ,
,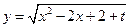 ,
, 的最小值恰好是方程:
的最小值恰好是方程: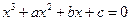 的三个根,其中
的三个根,其中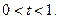
(1)求证: ;
;
(2)设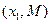 、
、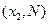 是函数
是函数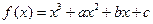 的两个极值点。
的两个极值点。
①若 ,求函数
,求函数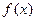 的解析式;
的解析式;
②求|M-N|的取值范围。
(本小题满分12分)已知函数
(1)若数列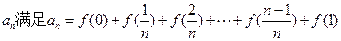 ,求数列
,求数列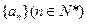 的通项公式;
的通项公式;
(2)若数列 ,则实数k为何值时,不等式
,则实数k为何值时,不等式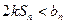 恒成立。
恒成立。
(本小题满分12分)已知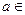 ,函数
,函数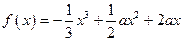 .
.
(Ⅰ)当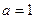 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)在上单调递减,求的取值范围;
(Ⅲ)若函数f(x)在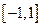 上单调递增,求的取值范围.
上单调递增,求的取值范围.