(本小题满分12分)
如图,圆 :
: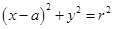
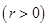 与抛物线
与抛物线 :
:
 的一个交点M
的一个交点M ,且抛物线在点M处的切线过圆心
,且抛物线在点M处的切线过圆心 .
. 
(Ⅰ)求 和
和 的标准方程;
的标准方程;
(Ⅱ)若点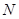 为抛物线
为抛物线 上的一动点,求
上的一动点,求 的取值范围.
的取值范围.
(本小题满分12分)如图,正三角形ABC与直角三角形BCD成直二面角,且∠BCD=90°,∠CBD=30°.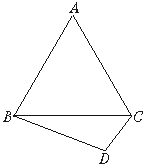
(1)求证:AB⊥CD;
(2)求二面角D—AB—C的大小;
(3)求异面直线AC和BD所成的角.
(本小题满分12分)数列{an}中,a1=1,n≥2时,其前n项的和Sn满足Sn2=an(Sn- ).
).
(1)求Sn的表达式;
(2)设bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(本小题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且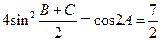 ,
,
(1)求∠A的度数;
(2)若a=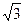 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
已知数列 中,
中, 且点
且点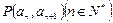 在直线
在直线 上.
上.
(1)求数列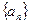 的通项公式;
的通项公式;
(2)若函数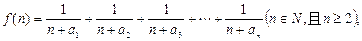 求函数
求函数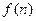 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于 的整式
的整式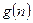 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出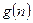 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本小题满分12分)如图,已知直线l: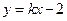 与抛物线C:
与抛物线C: 交于A,B两点,
交于A,B两点,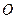 为坐标原点,
为坐标原点,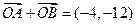 。
。
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,
求△ABP面积最大值.