一只甲虫在5×5的方格（每小格边长为1m）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫（A,B,C,D都在格点上）。规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（＋1，＋4），从B到A记为：A→B（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（ ， ），B→C（ ， ）,C→ （＋1， ）；
（2）若这只甲虫的行走路线为A→D→C→B，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋1），（＋3，2），（－2，-1），（－1，－2），请在图中标出P的位置。
(4) 在(3)中甲虫若每走1m需消耗1.5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?
计算：（1）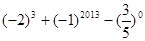
；（2）（3a＋5b）（－3a－8b）
解方程组：（1）
；（2）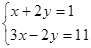
如图所示，已知∠1=∠2，∠3=85°，求∠4的度数．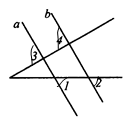
解：∵∠1=∠2（）
∴a∥b（）
∴∠3=∠4（）
∵∠3=85°（）
∴∠4=85°
如图(1)线段AB、CD相交于点O,连接AD、CB．如图(2),在图(1)的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．
试解答下列问题：
(1)在图(1)中,请直接写出∠A、∠B、∠C、∠D之间的等量关系；
(2)在图(2)中,若∠D=40°,∠B=30°,试求∠P的度数；（写出解答过程）
如图①是一个长为2a,宽为2b的长方形纸片,其长方形的面积显然为4ab,现将此长方形纸片沿图中虚线剪开,分成4个小长方形,然后拼成如图②的一个正方形.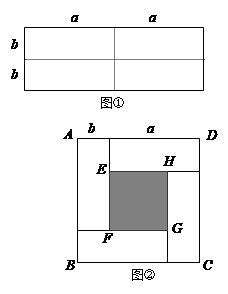
(1)图②中阴影正方形EFGH的边长为: _________________；
(2)观察图②,代数式(a -b)2表示哪个图形的面积？代数式(a+b)2呢？
(3)用两种不同方法表示图②中的阴影正方形EFGH的面积,并写出关于代数式(a+b)2、(a -b)2和4ab之间的等量关系；
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,求:(a -b)2的值.