甲、乙两名射击选手各自射击十组，按射击的时间顺序把每组射中靶的环数值记录如下表：
| 选手 组数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 甲 |
98 |
90 |
87 |
98 |
99 |
91 |
91 |
96 |
98 |
96 |
| 乙 |
85 |
91 |
89 |
97 |
96 |
97 |
98 |
96 |
98 |
98 |
（1）根据上表数据，完成下列分析表：
| |
平均数 |
众数 |
中位数 |
方差[ |
极差 |
| 甲 |
94.5 |
|
96 |
15.56 |
12 |
| 乙 |
94.5 |
|
|
18.65 |
|
（2）如果要从甲、乙两名选手中选择一个参加比赛，应选哪一个？为什么？
如图1，一扇窗户打开后用窗钩AB可将其固定．
（1）这里所运用的几何原理是（）
| A．三角形的稳定性 | B．两点之间线段最短 |
| C．两点确定一条直线 | D．垂线段最短 |
（2）图2是图1中窗子开到一定位置时的相关平面图，若∠OAB=45°，∠OBA=30°，
点O到AB边的距离为2cm，求窗钩AB的长（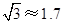
，结果精确到整数）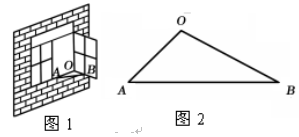
如图，在ΔABC中， BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，
（1）试叙述等式:∠1=∠2成立之理由;
（2）当BC="5" cm时，试求ΔPDE的周长CΔPDE.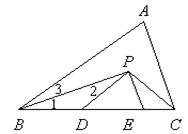
作图题，请你在下图中作出一个以线段AB为一边的一个等边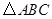
．
（要求：用尺规作图，并写出已知、求作，保留作图痕迹，不写作法和结论）
已知：
求作：
解不等式组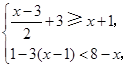
并写出该不等式组的整数解。
求不等式7－3x >0的解，并将其解表示在数轴上．