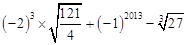如图,在△ABC中,∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.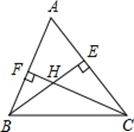
(本题8分)为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?
(本题7分)如图,AB∥CD,点P是直线AC和BD之间的一动点,当点P运动到某一位置时,连接PA,PB.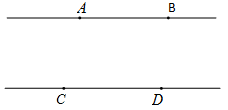
(1)当点P在运动过程中构成了不同类型的∠APC,试画出各种不同类型的∠APB.
(2)请直接写出∠APC,∠PAB,∠PCD之间的等量关系.
(本题6分)名著《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上的一只鸽子对地上觅食的鸽子说:“若从你们中飞上来一只,则树下的鸽子就是整个鸽群的 ; 若从树上飞下去一只,则树上、树下的鸽子就一样多了.”你知道树上、树下各有多少只鸽子吗?
; 若从树上飞下去一只,则树上、树下的鸽子就一样多了.”你知道树上、树下各有多少只鸽子吗?
(本题5分)解不等式组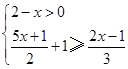
计算(每小题4分,共8分):
(1)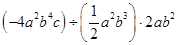
(2)