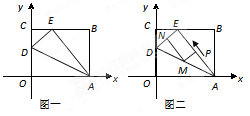
如图一,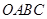 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,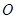 为原点,点
为原点,点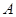 在
在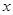 轴的正半轴上,点
轴的正半轴上,点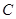 在
在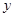 轴的正半轴上,
轴的正半轴上,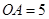 ,
,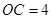 .
.
(1)在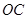 边上取一点
边上取一点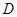 ,将纸片沿
,将纸片沿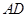 翻折,使点
翻折,使点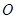 落在
落在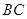 边上的点
边上的点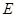 处,求
处,求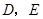 两点的坐标;
两点的坐标;
(2)如图二,若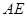 上有一动点
上有一动点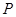 (不与
(不与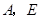 重合)自
重合)自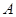 点沿
点沿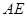 方向向
方向向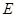 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为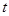 秒(
秒(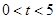 ),过
),过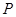 点作
点作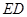 的平行线交
的平行线交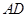 于点
于点 ,过点
,过点 作
作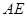 的平行线交
的平行线交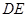 于点
于点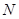 .求四边形
.求四边形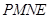 的面积
的面积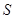 与时间
与时间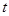 之间的函数关系式;当
之间的函数关系式;当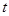 取何值时,
取何值时,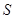 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)在(2)的条件下,当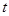 为何值时,以
为何值时,以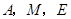 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点 的坐标.
的坐标.
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题
|
组别 |
学习时间x(h) |
频数(人数) |
|
A |
0<x≤1 |
8 |
|
B |
1<x≤2 |
24 |
|
C |
2<x≤3 |
32 |
|
D |
3<x≤4 |
n |
|
E |
4小时以上 |
4 |
(1)表中的n= ,中位数落在 组,扇形统计图中B组对应的圆心角为 °;
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
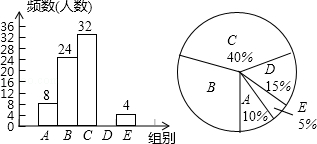
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2,并写出点C的对应点C2的坐标.
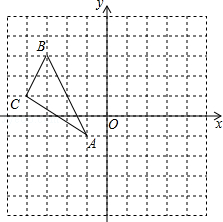
如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.

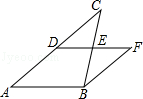
已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
