某蒜苔生产基地喜获丰收收蒜苔200吨。经市场调查,可采用批发、零售、冷库储藏后销售,并按这三种方式销售,计划每吨的售价及成本如下表:
| 销售方式 |
批发 |
零售 |
冷库储藏后销售 |
| 售价(元/吨) |
3000 |
4500 |
5500 |
| 成本(元/吨) |
700 |
1000 |
1200 |
若经过一段时间,蒜苔按计划全部售出后获得利润为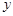 (元)蒜苔
(元)蒜苔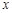 (吨),且零售是批发量的1/3.
(吨),且零售是批发量的1/3.
(1)求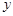 与
与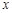 之间的函数关系?
之间的函数关系?
(2)由于受条件限制经冷库储藏的蒜苔最多80吨,求该生产基地计划全部售完蒜苔获得最大利润。
已知关于x的一元二次方程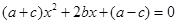 ,其中a、b、c分别为△ABC三边的长.
,其中a、b、c分别为△ABC三边的长.
(1)如果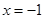 是方程的根,试判断△ABC的形状,并说明理由;
是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
如图,在平面直角坐标系中,一次函数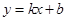 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数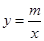 的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6,-1),DE=3.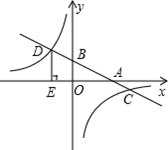
(1)求反比例函数与一次函数的解析式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
解方程:(每小题4分,共8分)
(1)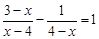 .
.
(2)
某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)直线AB上是否存在点C,使△BOC的面积为2?若存在,求出点C的坐标;若不存在,请说明理由.