(1)任选以下三个条件中的一个,求二次函数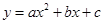 的解析式;
的解析式;
①y随x变化的部分数值规律如下表:
| x |
-1 |
0 |
1 |
2 |
3 |
| y |
0 |
3 |
4 |
3 |
0 |
②有序数对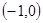 、
、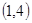 、
、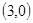 满足
满足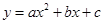 ;
;
③已知函数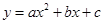 的图象的一部分(如图).
的图象的一部分(如图).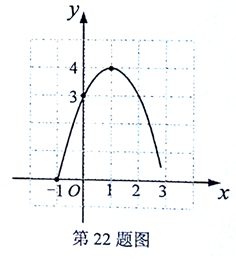
(2)直接写出二次函数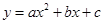 的三个性质.
的三个性质.
某初中学校对全校学生进行一次“勤洗手”的问卷调查,学校七、八、九三个年级学生人数分别为600人、700人、600人,经过数据整理将全校的“勤洗手”调查数据绘制成统计图.
(1)根据统计图,计算八年级“勤洗手”学生人数,并补全下列两幅统计图.
(2)通过计算说明那个年级“勤洗手”学生人数占本年级学生人数的比例最大?
解方程: .
.
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,
∠FDE=90°,DF=4,DE=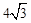 。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。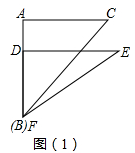
(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=度;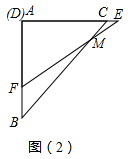
(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;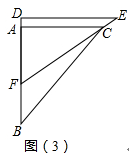
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围。
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.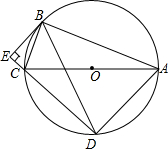
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线。
已知二次函数
.
(1)当二次函数的图象经过坐标原点
时,求二次函数的解析式;
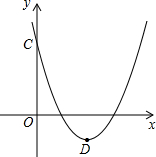
(2)如图,当
时,该抛物线与
轴交于点
,顶点为
,求
、
两点的坐标;
(3)在(2)的条件下,
轴上是否存在一点
,使得
最短?若
点存在,求出
点的坐标;若
点不存在,请说明理由。