规律是数学研究的重要内容之一．
初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面．请你解决以下与数的表示和运算相关的问题：
(1)写出奇数a用整数n表示的式子；
(2)写出有理数b用整数m和整数n表示的式子；
(3)函数的研究中，应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律)．
下面对函数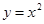
的某种数值变化规律进行初步研究：
 |
0 |
1 |
2 |
3 |
4 |
5 |
... |
 |
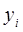0 |
1[ |
4 |
9 |
16 |
25 |
... |
 |
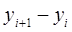1 |
3 |
5 |
7 |
9 |
11 |
... |
由表看出，当x的取值从0开始每增加1个单位时，y的值依次增加1，3，5...
请回答：
①当x的取值从0开始每增加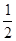
个单位时，y的值变化规律是什么？
②当x的取值从0开始每增加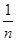
个单位时，y的值变化规律是什么？
已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
8 |
3 |
0 |
-1 |
0 |
3 |
… |
(1) 求该二次函数的解析式；
(2) 当x为何值时，y有最小值，最小值是多少？
(3)
若A（m,y1）,B(m+2, y2)两点都在该函数的图象上，计算当m取何值时，
在平面直角坐标系xoy中，已知
三个顶点的坐标分别为
⑴ 画出
；⑵ 画出
绕点
顺时针旋转
后得到的
，并求出
的长.
如图，在△ABC中，点D在边AB上，满足且∠ACD =∠ABC，若AC = 2，AD =1，求DB
的长.
已知排水管的截面为如图所示的圆
,半径为10，圆心到水面的距离是6，求水面宽
.
解方程： .