某公司为了提高经济效益,决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作。经调查发现:分工后,留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍。已知某公司现有员工50人,设抽调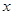 人到新生产线上工作。
人到新生产线上工作。
(1)若分工前员工每月的人均产值为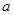 元,则分工后留在原生产线上工作的员工每月人均产值是 元,每月的总产值是 元;到新生产线上工作的员工每月人均产值是
元,则分工后留在原生产线上工作的员工每月人均产值是 元,每月的总产值是 元;到新生产线上工作的员工每月人均产值是
元,每月的总产值是 元。
(2)分工后若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值,而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半。
问:抽调的人数应该在什么范围?
在一个不透明的袋子中,装有除颜色外其余均相同的红、黄、蓝三种球,其中有2个红球、1个蓝球,从中任意摸出一个是红球的概率为0.5
(1)求袋中有几个黄球;
(2)一手同时摸出两球(相当于第一次随机摸出一球,不放回,再随机摸出第二个球),请用画树状图或列表法求摸到两球至少一个球为红球的概率.
“你今天光盘了吗?”这是国家倡导厉行节约,反对浪费以来的时尚流行语,某校团委随机抽取部分了学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如下,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题:
(1)求本次活动共调查了多少名学生?
(2)请补全图2,并求出图1中,B区域的圆心角度数;
(3)若该校有2400名学生,请估算该校不是了解很多的学生人数.
如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.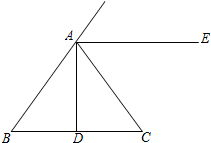
(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
已知x2+4x-1=0,求代数式(2x+1)2-(x+2)(x-2)-x(x-4)的值.
(1)计算:(1- )0-tan60°+(
)0-tan60°+( )-1
)-1
(2)解方程组: .
.