(本小题满分14分)已知函数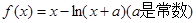 .
.
(1)求函数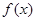 的单调区间;
的单调区间;
(2)当 处取得极值时,若关于
处取得极值时,若关于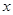 的方程
的方程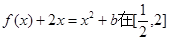 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)求证:当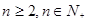 时,有
时,有
(本题满分12 分)
(1)计算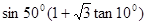 ,
,
(2)已知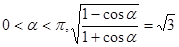 ,求sin
,求sin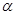 的值。
的值。
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=-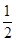 对称,且f′(1)=0.
对称,且f′(1)=0.
(1)求实数a,b的值;
(2)讨论函数f(x)的单调性,并求出单调区间 。
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小
(3)求点C到平面PBD的距离.
(本题满分13分)
已知椭圆C的两焦点分别为 ,长轴长为6,
,长轴长为6,
⑴求椭圆C的标准方程;
⑵已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。
(本题满分12分)
如图,已知三棱锥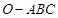 的侧棱
的侧棱 两两垂直,
两两垂直,
且 ,
,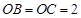 ,
, 是
是 的中点。
的中点。
(1)求异面直线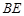 与
与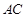 所成角的余弦值;
所成角的余弦值;
(2)求直线BE和平面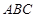 的所成角的正弦值。
的所成角的正弦值。