如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.

(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小
(3)求点C到平面PBD的距离.
已知 ;
; .
.
(1)若p是q的必要条件,求m的取值范围;
(2)若 是
是 的必要不充分条件,求m的取值范围.
的必要不充分条件,求m的取值范围.
已知圆C经过点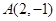 ,和直线
,和直线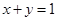 相切,且圆心在直线
相切,且圆心在直线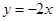 ,求圆C的方程.
,求圆C的方程.
三棱锥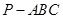 的侧棱PA、PB、PC两两互相垂直,且
的侧棱PA、PB、PC两两互相垂直,且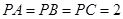 ,则三棱锥
,则三棱锥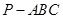 的外接球的体积是()
的外接球的体积是()
A.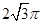 B.
B.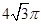 C.
C.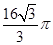 D.
D.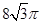
已知椭圆C的方程是
 的离心率为
的离心率为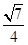 ,长轴长为8.
,长轴长为8.
(1)求椭圆C的标准方程;
(2)若不垂直于坐标轴的直线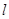 经过点
经过点 ,与椭圆C交于A,B两点,设点Q的坐标为
,与椭圆C交于A,B两点,设点Q的坐标为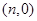 ,直线AQ,BQ的斜率之和为0,求mn的值.
,直线AQ,BQ的斜率之和为0,求mn的值.
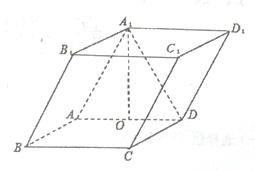
如图,四棱柱 中,底面ABCD是矩形,且
中,底面ABCD是矩形,且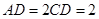 ,
,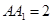 ,
,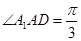 ,若O为AD的中点,且
,若O为AD的中点,且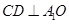 .
.
(1)求证: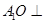 平面ABCD;
平面ABCD;
(2)线段BC上是否存在一点P,使得二面角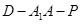 为
为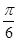 ?若存在,求出BP的长;不存在,说明理由.
?若存在,求出BP的长;不存在,说明理由.