如图，在平面直角坐标系中，已知点
坐标为（2，4），直线
与
轴相交于点
，连结
，抛物线
从点
沿方向平移，与直线交于点
，顶点
到点时停止移动．
（1）求线段所在直线的函数解析式；
（2）设抛物线顶点的横坐标为
，
①用的代数式表示点的坐标；
②当为何值时，线段
最短；
（3）当线段最短时，相应的抛物线上是否存在点
，使△
的面积与△
的面积相等，若存在，请求出点的坐标；若不存在，请说明理由．
将一副三角尺按照如图的位置摆放，使得三角尺ACB的直角顶点C在三角尺DEF的直角边EF上．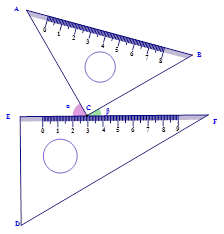
(1)求∠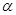
十∠
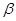的度数；
(2)若∠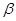=32°，试问∠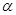的补角为多少度？
先化简后求值，2x-5(x-2y)+6x(1-3y)，其中x=4，y=-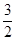
解方程：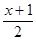
=2+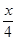
计算：-2+4÷（-2）
如图（1），一正方形纸板ABCD的边长为4，对角线AC、BD交于点O，一块等腰直角三角形的三角板的一个顶点处于点O处，两边分别与线段AB、AD交于点E、F，设BE=
．
（1）若三角板的直角顶点处于点O处，如图（2）．判断三角形EOF的形状
，并说明理由。
（2）在（1）的条件下，若三角形EOF的面积为S，求S关于x的函数关系式。
（3）若三角板的锐角顶点处于点O处，如图（3）．
①若DF=
，求关于的函数关系式，并写出自变量的取值范围；
②探究直线EF与正方形ABCD的内切圆的位置关系，并证明你的结论．