如图,直线 与x轴、y轴分别相交于点A、B,与正比例函数
与x轴、y轴分别相交于点A、B,与正比例函数 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
(1)△CDE是 ▲ 三角形;点C的坐标为 ▲ ,点D的坐标为 ▲ (用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线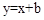 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。
已知抛物线 与
与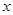 轴交于点A(
轴交于点A(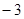 ,0),
,0),
(1)直接写出抛物线与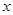 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)若直线过抛物线顶点M及抛物线与 轴的交点
轴的交点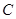 (0,3).
(0,3).
① 求直线MC所对应的函数关系式;
② 若直线MC与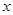 轴的交点为
轴的交点为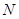 ,在抛物线上是否存在点
,在抛物线上是否存在点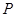 ,使得△NPC是以NC为直角边的直角三角形?若存在,求出点
,使得△NPC是以NC为直角边的直角三角形?若存在,求出点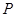 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 
某电器商城“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示
| 类别 |
冰箱 |
彩电 |
| 进价(元/台) |
2320 |
1900 |
| 售价(元/台) |
2420 |
1980 |
(1)按国家政策,农民购买“家电下乡”产品享受售价13℅的政府补贴。农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的补贴?
(2)为满足农民需求,商场决定用不超过85000元采购冰箱、彩电共40台,且冰箱的数量不少于彩电数量的 . 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
. 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
如图,在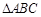 中,
中,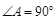 ,
,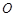 是
是 边上一点,以
边上一点,以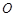 为圆心的半圆分别与
为圆心的半圆分别与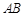 、
、 边相切于
边相切于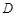 、
、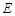 两点,连接
两点,连接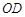 .已知
.已知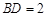 ,
, .求:
.求: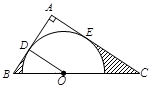
(1)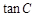 ;
;
(2)图中两部分阴影面积的和.
在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数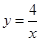 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x、y满足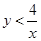 的概率.
的概率.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1.
(1)证明:△A1AD1≌△CC1B;
(2)若∠ACB=30°,试问当点C1在线段AC上的什么位置时,四边形ABC1D1是菱形. (直接写出答案)