随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如右图所示.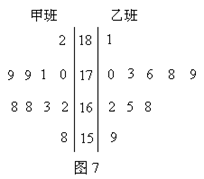
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求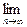 xn
xn
据有关资料,1995年我国工业废弃垃圾达到7.4×108吨,占地562.4平方公里,若环保部门每年回收或处理1吨旧物资,则相当于处理和减少4吨工业废弃垃圾,并可节约开采各种矿石20吨,设环保部门1996年回收10万吨废旧物资,计划以后每年递增20%的回收量,试问:
(1)2001年回收废旧物资多少吨?
(2)从1996年至2001年可节约开采矿石多少吨(精确到万吨)?
(3)从1996年至2001年可节约多少平方公里土地?
某公司全年的利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第1位职工得奖金 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设ak(1≤k≤n)为第k位职工所得奖金金额,试求a2,a3,并用k、n和b表示ak(不必证明);
(2)证明ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
(3)发展基金与n和b有关,记为Pn(b),对常数b,当n变化时,求 Pn(b).
Pn(b).
已知数列{an}满足条件: a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,设bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范围;
(2)求bn和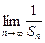 ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;
(3)设r=219.2-1,q=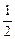 ,求数列{
,求数列{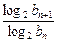 }的最大项和最小项的值.
}的最大项和最小项的值.
设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4…).
(1)求证: 数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(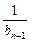 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn;
(3)求和: b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1.