已知数列 为等比数列,其前
为等比数列,其前 项和为
项和为 ,已知
,已知 ,且对于任意的
,且对于任意的 有
有 ,
, ,
, 成等差;
成等差;
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)已知 (
( ),记
),记 ,若
,若 对于
对于 恒成立,求实数
恒成立,求实数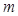 的范围.
的范围.
某年级的10名班长中有8名女生,现从中选派5人参加友好学校访谈活动.用X表示选派的女班长人数.
(1)求有男班长参加的概率;(2)求X的分布列和期望.
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数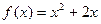 的图象上,且过点
的图象上,且过点 的切线的斜率为
的切线的斜率为 .
.
(1)求数列 的通项公式;(2)若
的通项公式;(2)若 ,求数列
,求数列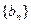 的前
的前 项和
项和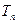 ;
;
(3)设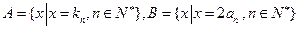 ,等差数列
,等差数列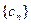 的任一项
的任一项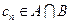 ,其中
,其中 是
是 中的最小数,
中的最小数,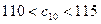 ,求
,求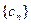 的通项公式.
的通项公式.
已知函数 ,其中
,其中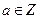 .
.
(1)讨论函数f(x)的单调性;(2)当 时,求函数f(x)的最大值.
时,求函数f(x)的最大值.
(本小题满分12分)
已知数列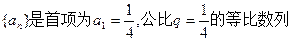 ,设
,设 ,数列
,数列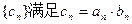 。(1)求证:
。(1)求证: 是等差数列; (2)求数列
是等差数列; (2)求数列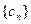 的前n项和Sn;
的前n项和Sn;
(3)若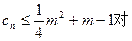 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
(本小题满分12分)
某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交 元(
元( 为常数,
为常数,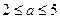 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与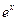 (
( 为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润
为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润 元与每件产品的日售价
元与每件产品的日售价 元的函数关系式;当每件产品的日售价为多少元时该商店的日利润
元的函数关系式;当每件产品的日售价为多少元时该商店的日利润 最大,说明理由。
最大,说明理由。