若函数y=ax与y=-
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( )
| A．增函数 | B．减函数 | C．先增后减 | D．先减后增 |
函数f(x)=1-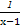
( )
| A．在(-1,+∞)上单调递增 |
| B．在(1,+∞)上单调递增 |
| C．在(-1,+∞)上单调递减 |
| D．在(1,+∞)上单调递减 |
给定函数①y=
,②y=lo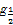
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上是单调递减的函数的序号是( )
| A．①② | B．②③ | C．③④ | D．①④ |
函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是( )
| A．(-∞,0],(-∞,1] | B．(-∞,0],[1,+∞) |
| C．[0,+∞),(-∞,1] | D．[0,+∞),[1,+∞) |
已知函数y=f(x)的图象关于直线x=-1对称,且当x∈(0,+∞)时,有f(x)=
,则当x∈(-∞,-2)时,f(x)的解析式为( )
| A．f(x)=- |
B．f(x)=- |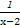
C．f(x)= |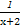
D．f(x)=- |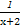
