(本小题满分14分)
已知函数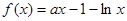
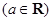 .
.
(1)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数 在
在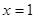 处取得极值,对
处取得极值,对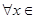
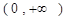 ,
,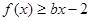 恒成立,求实数
恒成立,求实数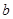 的取值范围;
的取值范围;
(3)当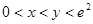 且
且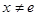 时,试比较
时,试比较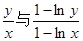 的大小.
的大小.
如图,在正方体ABCD-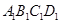 中,棱长为a,E为棱CC1上的的动点.
中,棱长为a,E为棱CC1上的的动点.
(1)求证:A1E⊥BD;
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD.
已知某几何体的直观图和三视图如图所示,其正(主)视图为矩形,侧(左)视图为等腰直角三角形,俯视图为直角梯形.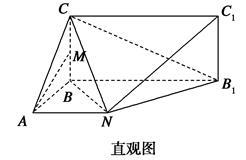
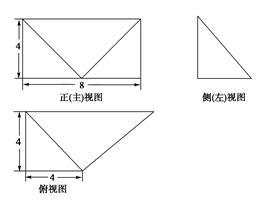
(1)若M为CB中点,证明:MA∥平面CNB1;
(2)求这个几何体的体积.
三棱锥P—ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证:
(1)AO⊥BC
(2)PB⊥AC
如图,正方体的棱长为a,P、Q分别为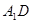 、
、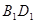 的中点
的中点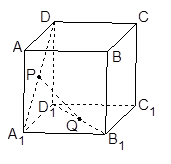
(1)求证:PQ∥平面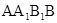
(2)求PQ的长
已知函数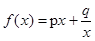 (实数p、q为常数),且满足
(实数p、q为常数),且满足 .
.
(1)求函数 的解析式;
的解析式;
(2)试判断函数 在区间
在区间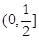 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)当 时,函数
时,函数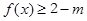 恒成立,求实数m的取值范围
恒成立,求实数m的取值范围