如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.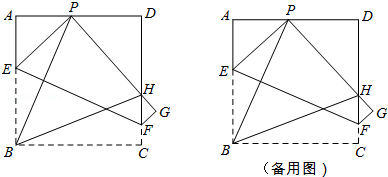
“绿水青山就是金山银山”,为保护生态环境, , 两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
|
村庄 |
清理养鱼网箱人数 人 |
清理捕鱼网箱人数 人 |
总支出 元 |
|
|
15 |
9 |
57000 |
|
|
10 |
16 |
68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒 ;③ 型尺 所在的直线垂直平分线段 .
(1)在图1中,请你画出用 形尺找大圆圆心的示意图(保留画图痕迹,不写画法);
(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:
将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点 , 之间的距离,就可求出环形花坛的面积.”如果测得 ,请你求出这个环形花坛的面积.

某校开展研学旅行活动,准备去的研学基地有 (曲阜)、 (梁山)、 (汶上), (泗水),每位学生只能选去一个地方,王老师对本班全体同学选取的研学基地情况进行调查统计,绘制了两幅不完整的统计图(如图所示).
(1)求该班的总人数,并补全条形统计图.
(2)求 (泗水)所在扇形的圆心角度数;
(3)该班班委4人中,1人选去曲阜,2人选去梁山,1人选去汶上,王老师要从这4人中随机抽取2人了解他们对研学基地的看法,请你用列表或画树状图的方法,求所抽取的2人中恰好有1人选去曲阜,1人选去梁山的概率.

如图1,抛物线 过 、 两点,交 轴于点 ,过点 作 轴的平行线与抛物线上的另一个交点为 ,连接 、 .点 是该抛物线上一动点,设点 的横坐标为 .
(1)求该抛物线的表达式和 的正切值;
(2)如图2,若 ,求 的值;
(3)如图3,过点 、 的直线与 轴于点 ,过点 作 ,垂足为 ,直线 与 轴交于点 ,试判断四边形 的形状,并说明理由.

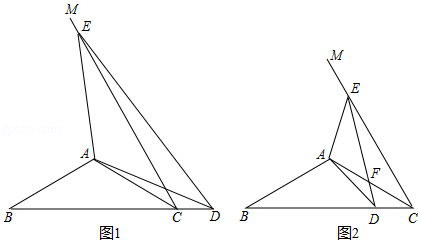
在 中, , ,以 为边在 的另一侧作 ,点 为射线 上任意一点,在射线 上截取 ,连接 、 、 .
(1)如图1,当点 落在线段 的延长线上时,直接写出 的度数;
(2)如图2,当点 落在线段 (不含边界)上时, 与 交于点 ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若 ,求 的最大值.