(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
如图,直线y=kx+2与x轴、y轴分别交于点A、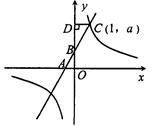
B,点C(1,a)是直线与双曲线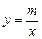 的一个交点,过点C作
的一个交点,过点C作
CD⊥y轴,垂足为D,且△BCD的面积为1.
(1)求双曲线的解析式 与直线AB的解析式:
与直线AB的解析式:
(2)若在y轴上有一点E,使得以E、A、B为顶点的三角形与
△BCD相似,求点E的坐标.
现有一张宽为12cm练习纸,相邻两条格线间的距离均为0.8cm.调皮的小聪在
纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上,测得∠a=32°.
(1)求矩形图案的面积:
(2)若小聪在第一个图案的右边以同样的方式继续盖印(如图),最多一共能印几个完整的图
案?(参考数据:sin32 °≈0.5,cos32°≈0.8,tan32°≈0.6)
°≈0.5,cos32°≈0.8,tan32°≈0.6)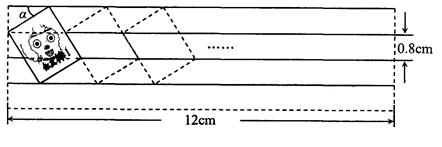
如图,函数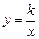 (x>0,k为常数)的图象经过
(x>0,k为常数)的图象经过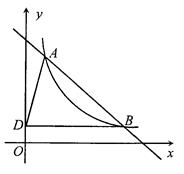
A(1,4),B(m,n), 其中m>1,过点B作y轴的垂线,垂
其中m>1,过点B作y轴的垂线,垂
足为D,连结AD.
(1)求k的值;
(2)若△ABD的面积为4,求点B的坐标;并回答当x取何
值时,直线AB的图象在反比例函数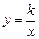 图象的上方.
图象的上方.
某市今年1月份起调整居民用水价格,每立方米水费上涨25%,小明家去年12
月份的水费是18元,而今年5月份的水费是36元,已知小明家今年5月份的用水量比12
月份多6 m3,求该市今年居民用水的价格.
已知梯形ABCD中,AD∥BC,∠A=90°,点E为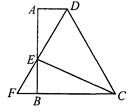
AB上一点,且CE⊥DE,CB、DE的延长线交于点F.
(1)求证: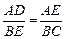 ;
;
(2)已知EF=5,FB=3,求BC的长.