问题提出：以n边形的n个顶点和它内部的m个点，共(m＋n)个点作为顶
点，可把原n边形分割成多少个互不重叠的小三角形？
问题探究：为了解决上面的问题，我们将采取一般问题特殊化的策略，先从简单和具体的情形入手：
探究一：以△ABC的3个顶点和它内部的1个点P，共4个点为顶点，可把△ABC分割成多少个互
不重叠的小三角形？如图①，显然，此时可把△ABC分割成3个互不重叠的小三角形．
探究二：以△ABC的3个顶点和它内部的2个点P、Q，共5个点为顶点，可把△ABC分割成多少个
互不重叠的小三角形？
在探究一的基础上，我们可看作在图①△ABC的内部，再添加1个点Q，那么点Q的位置会有两种
情况：
一种情况，点Q在图①分割成的某个小三角形内部．不妨设点Q在△PAC的内部，如图②；
另一种情况，点Q在图①分割成的小三角形的某条公共边上．不妨设点Q在PA上，如图③．
显然，不管哪种情况，都可把△ABC分割成5个互不重叠的小三角形．
探究三：以△ABC的三个顶点和它内部的3个点P、Q、R，共6个点为顶点，可把△ABC分割成 个
互不重叠的小三角形，并在图④中画出一种分割示意图．
探究四：以△ABC的三个顶点和它内部的m个点，共(m＋3)个点为顶点，可把△ABC分割成 个
互不重叠的小三角形．
探究拓展：以四边形的4个顶点和它内部的m个点，共(m＋4)个点为顶点，可把四边形分割成
个互不重叠的小三角形．
问题解决：以n边形的n个顶点和它内部的m个点，共(m＋n)个点作为顶点，可把原n边形分割成
个互不重叠的小三角形．
实际应用：以八边形的8个顶点和它内部的2012个点，共2020个顶点，可把八边形分割成多少个互
不重叠的小三角形？(要求列式计算)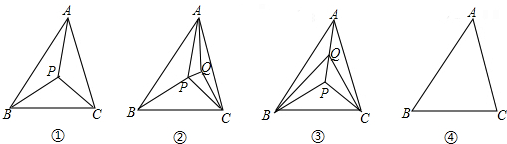
“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗，我市某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽（以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查结果绘制成如下两幅统计图．
请根据以上信息回答：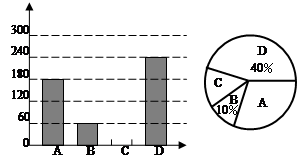
（1）本次参加抽样调查的居民有多少人？
（2）将不完整的条形图补充完整．
（3）若居民区有8000人，请估计爱吃D 粽的人数？
（4）若有外型完全相同的A、B、C、D粽各一个煮熟后，小王吃了两个，用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率？
数学课上，老师和同学们对矩形纸片进行了图形变换的以下探究活动：
（1）如图1，若连接矩形ABCD的对角线AC、BD相交于点O，则Rt△ADC可由Rt△ABC经过旋转变换得到，这种旋转变换的旋转中心是点、旋转角度是°；
（2）如图2，将矩形纸片ABCD沿折痕EF对折、展平．再沿折痕GC折叠，使点B落在EF上的点B′处，这样能得到∠B′GC．求∠B′GC的度数．
（3）如图3，取AD边的中点P，剪下△BPC，将△BPC沿着射线BC的方向依次进行平移变换，每次均移动BC的长度，得到了△CDE、△EFG和△GHI（如图4）．若BH=BI，BC=a，则：①证明以BD、BF、BH为三边构成的新三角形的是直角三角形；②若这个新三角形面积小于50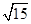
，请求出a的最大整数值．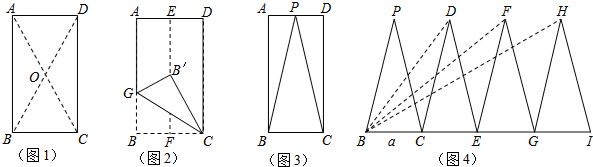
如图，已知关于x的二次函数y=x2+mx的图象经过原点O，并且与x轴交于点A，对称轴为直线x=1．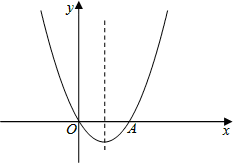
（1）常数m=，点A的坐标为；
（2）若关于x的一元二次方程x2+mx=n（n为常数）有两个不相等的实数根，求n的取值范围；
（3）若关于x的一元二次方程x2+mx-k=0（k为常数）在-2＜x＜3的范围内有解，求k的取值范围．
甲、乙两家超市进行促销活动，甲超市采用“买100减50”的促销方式，即购买商品的总金额满100元但不足200元，少付50元；满200元但不足300元，少付100元；…．乙超市采用“打6折”的促销方式，即顾客购买商品的总金额打6折．
（1）若顾客在甲商场购买商品的总金额为x（100≤x＜200）元，优惠后得到商家的优惠率为p（p=
），写出p与x之间的函数关系式，并说明p随x的变化情况；
（2）王强同学认为：如果顾客购买商品的总金额超过100元，实际上甲超市采用“打5折”、乙超市采用“打6折”，那么当然选择甲超市购物．请你举例反驳；
（3）品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x（300≤x＜400）元，认为选择哪家商场购买商品花钱较少？请说明理由．
（1）如图1，4条直线l1、l2、l3、l4是一组平行线，相邻2条平行线的距离都是2cm，正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上，求该正方形的面积；
（2）如图2，把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中，恰好四个顶点都在横格线上，已知∠1=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0．60，cos36°≈0．80，tan36°≈0．75）