数学课上，老师和同学们对矩形纸片进行了图形变换的以下探究活动：
（1）如图1，若连接矩形ABCD的对角线AC、BD相交于点O，则Rt△ADC可由Rt△ABC经过旋转变换得到，这种旋转变换的旋转中心是点 、旋转角度是 °；
（2）如图2，将矩形纸片ABCD沿折痕EF对折、展平．再沿折痕GC折叠，使点B落在EF上的点B′处，这样能得到∠B′GC．求∠B′GC的度数．
（3）如图3，取AD边的中点P，剪下△BPC，将△BPC沿着射线BC的方向依次进行平移变换，每次均移动BC的长度，得到了△CDE、△EFG和△GHI（如图4）．若BH=BI，BC=a，则：①证明以BD、BF、BH为三边构成的新三角形的是直角三角形；②若这个新三角形面积小于50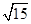
，请求出a的最大整数值．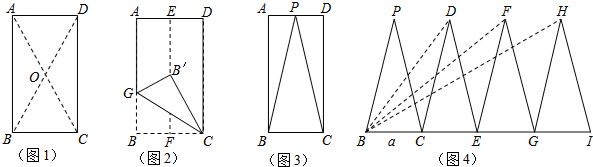
如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．在△ABC外有一点F，使FA⊥AE，FC⊥BC．
（1）求证：BE=CF；
（2）在AB上取一点M，使BM=2DE，连接MC，交AD于点N，连接ME．
求证：①ME⊥BC；②CM平分∠ACE．
如图，正方形ABCD中，CD＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．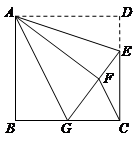
（1）求证：①△ABG≌△AFG； ②求GC的长；
（2）求△FGC的面积．
某超市计划购进一批甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元．
（1）求每件甲种、乙种玩具的进价分别是多少元？
（2）如果购进甲种玩具有优惠，优惠方法是：购进甲种玩具超过20件，超出部分可以享受7折优惠，若超市购进x（x＞0）件甲种玩具需要花费y元，求y与x的函数关系式；
（3）超市打算购买x件（x＞20）玩具，在（2）的条件下，从甲、乙两种玩具中选购其中一种，问：当x满足什么条件时超市购进甲种玩具比购进乙种玩具更省钱？
如图，在△ABC中，AB=5，AD=4，BD=DC=3，且DE⊥AB于E，DF⊥AC于点F．
（1）请写出与A点有关的三个正确结论；
（2）DE与DF在数量上有何关系？并给出证明．
如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．
（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．