半径分别为r=0.1m和R=2r=0.2m的两个质量不计的圆盘,共轴固定连接在一起,可以绕水平轴O无摩擦转动,大圆盘的边缘上固定有一个可看作质点的质量m=0.1kg的小球A,小圆盘上绕有细线,细线的另一端与放在光滑绝缘水平桌面上的带电小物块B水平相连,物块B的质量M=0.12kg,带电量为q=1.0×10-4C,处于水平向左的匀强电场中,电场强度大小为E0=104N/C。整个系统在如图所示位置处于静止平衡状态,此时OA连线与竖直方向的夹角为θ。求:

(1)夹角θ的大小。
(2)缓慢顺时针转动圆盘,使小球A位于转轴O的正下方由静止释放,当圆盘转过45º角时物块B运动的速度多大?
(3)缓慢顺时针转动圆盘,使小球A重新回到转轴O的正下方,改变电场强度大小使其为E后由静止释放系统,物块B向左运动的最大距离s=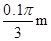 ,则电场强度E多大?
,则电场强度E多大?
带电为+3×106C的粒子先后经过电场中的A、B两点,该过程粒子克服电场力做功6×104J,已知B点电势为50V,求
(1)该粒子的电势能增加或减少了多少?
(2)A、B间两点间的电势差。
(3)A点的电势。
(4)另一电量为-3×106C的电荷在A点具有的电势能。
湖南省电视台“智勇大冲关”游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论。如图(13)所示,他们将选手简化为质量m=60kg的质点,选手抓住绳子末端由静止开始摆动,此时绳与竖直方向夹角 =53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
=53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
(1)选手摆到最低点时对绳拉力的大小F;
(2)选手摆到右边最高点时松手,选手将做什么运动?设水对选手的平均浮力 ,平均阻力
,平均阻力 ,求选手落入水中的深度
,求选手落入水中的深度 ;
;
(3)若要求选手摆到最低点时松手,且运动到浮台处离岸水平距离最大,则选手应将手握住绳子上离O点多长处?
我国分别于2007年10月24日和2010年10月1日成功发射“嫦娥一号”和“嫦娥二号”月球探测卫星,标志着我国实施绕月探测工程迈出重要一步,在政治、经济、军事、科技乃至文化领域都具有非常重大的意义,同学们也对月球有了更多的关注。
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径r1;
(2)若将来我国的宇航员随登月飞船登陆月球后,宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图(12)所示,现给小球一瞬间水平速度V,小球刚好能在竖直面内做完整的圆周运动。已知圆弧轨道半径为r,月球的半径为RO,万有引力常量为G,试求出月球的质量M月。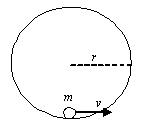
2008年12月,我国北方连降大雪,出现了罕见的雪灾。为了安全行车,某司机在冰雪覆盖的平直公路上测试汽车的制动性能。他从车上速度表看到汽车速度 时紧急刹车,由于车轮与冰雪公路面的摩擦,车轮在公路面上划出一道长L=50m的刹车痕后停止,取重力加速度g=10m/s2。求:
时紧急刹车,由于车轮与冰雪公路面的摩擦,车轮在公路面上划出一道长L=50m的刹车痕后停止,取重力加速度g=10m/s2。求:
(1)车轮与冰雪公路面间的动摩擦因数 ;
;
(2)该司机驾车以12m/s的速度在相同的冰雪水平路面上匀速行驶,突然发现前方停着一辆故障车。若刹车过程司机的反应时间为 ,为了避免两车相撞,该司机至少应在距故障车多远处发现故障车并采取同样的紧急刹车措施?
,为了避免两车相撞,该司机至少应在距故障车多远处发现故障车并采取同样的紧急刹车措施?
如图所示,光滑水平直轨道上有三个滑块 、
、 、
、 ,质量分别为
,质量分别为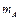 =
= =2
=2 ,
, =
= ,
,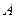 、
、 用细绳连接,中间一压缩的轻弹簧(弹簧与。滑块不栓接),开始时
用细绳连接,中间一压缩的轻弹簧(弹簧与。滑块不栓接),开始时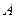 、
、 以共同速度
以共同速度 运动,
运动,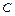 静止,某时刻细绳突然断开,
静止,某时刻细绳突然断开,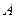 、
、 被弹开,然后
被弹开,然后 又与
又与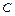 发生碰撞并粘在一起,最终三滑块速度恰好相同,求
发生碰撞并粘在一起,最终三滑块速度恰好相同,求 与
与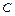 碰撞前
碰撞前 的速度。
的速度。