如图,在等腰梯形ABCD中,∠B=60º,且AB=AD=CD,请你将等腰梯形分成3个三角形,
使得其中有两个是相似三角形,且相似比不为1.
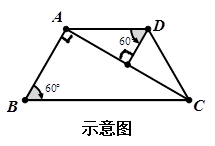
现在请你参考示意图,另外再给出三种分割方法(注:在两个相似三角形中标明必要的角度.)
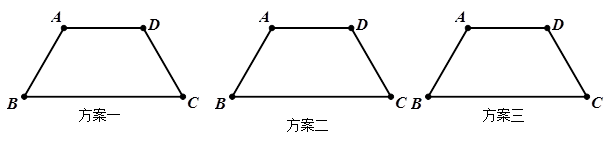
为了解今年全县2000名初四学生“创新能力大赛”的笔试情况.随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为 ;
(2)在表中:m= ;n= ;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么你估计该县初四学生笔试成绩的优秀人数大约是 名.
| 分数段 |
频数 |
频率 |
| 60≤x<70 |
30 |
0.1 |
| 70≤x<80 |
90 |
n |
| 80≤x<90 |
m |
0.4 |
| 90≤x<100 |
60 |
0.2 |
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
(1)画出将△ABC向右平移3个单位后得到的△A1B1C1,再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到的△A2B1C2;
(2)求线段B1C1旋转到B1C2的过程中,点C1所经过的路径长.
如图,在△ABC中,AD⊥BC于点D,AB=8,∠ABD=30°,∠CAD=45°,求BC的长.
如图①,在▱ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.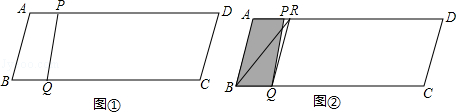
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2 与x轴交于点A(﹣1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.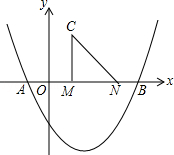
(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为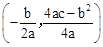 )
)