为了解今年全县2000名初四学生“创新能力大赛”的笔试情况.随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为 ;
(2)在表中:m= ;n= ;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么你估计该县初四学生笔试成绩的优秀人数大约是 名.
| 分数段 |
频数 |
频率 |
| 60≤x<70 |
30 |
0.1 |
| 70≤x<80 |
90 |
n |
| 80≤x<90 |
m |
0.4 |
| 90≤x<100 |
60 |
0.2 |
AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.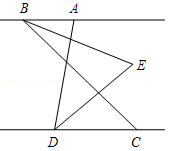
(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.
某工厂第一季度生产甲、乙两种机器共480台.改进生产技术后,计划第二季度生产这两种机器共554台,其中甲种机器产量要比第一季度增产10%,乙种机器产量要比第一季度增产20%.该厂第一季度生产甲、乙两种机器各多少台?
如图,若AD∥BC,∠A=∠D.
(1)猜想∠C与∠ABC的数量关系,并说明理由;
(2)若CD∥BE,∠D=50°,求∠EBC的度数.
小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
| 项目 |
月功能费 |
基本话费 |
长途话费 |
短信费 |
| 金额/元 |
5 |
50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?
如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.