某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形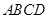 和
和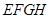 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为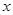 米,试求
米,试求 关于
关于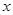 的函数关系式;
的函数关系式;
⑵当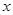 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.
已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=∅,求实数m的取值范围.
已知集合A={x| ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
已知集合M={x|x(x-a-1)<0,x∈R},N={x|x2-2x-3≤0},若M∪N=N,求实数a的取值范围.
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
已知椭圆 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率 .
.
(1)求椭圆的方程;
(2)若点 为曲线
为曲线 :
: 上任一点(
上任一点( 点不同于
点不同于 ),直线
),直线 与直线
与直线 交于点
交于点 ,
, 为线段
为线段 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.