(本小题13分)
如图,甲船以每小时 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 的方向
的方向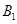 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达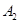 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西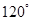 方向的
方向的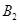 处,此时两船相距
处,此时两船相距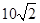 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
((本小题满分14分)如图,四棱锥 的底面
的底面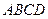 是正方形,侧棱
是正方形,侧棱
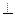 底面
底面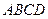 ,
,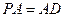 ,
, 、
、 分别是棱
分别是棱 、
、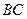 的中点.
的中点.
(1)求证: ;(2) 求直线
;(2) 求直线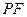 与平面
与平面 所成的角的正切值
所成的角的正切值
(本小题满分14分)等比数列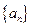 的各项均为正数,且
的各项均为正数,且
(1)求数列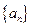 的通项公式.
的通项公式.
(2)设  求数列
求数列 的前
的前 项和.
项和.
(本小题满分14分)设
(1)求函数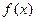 的单调递增
的单调递增 区间;
区间;
(2)在 中,若
中,若 ,且
,且 ,
, ,求
,求 的面积.
的面积.
已知函数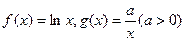 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 )图象上任意一点
)图象上任意一点 为切点的切线的斜率
为切点的切线的斜率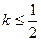 恒
恒
成立,求实数 的最小值。
的最小值。
(Ⅲ)是否存在实数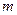 ,使得函数
,使得函数 的图象与
的图象与 的图象恰
的图象恰
好有四个不同的交点?若存在,求出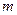 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为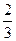 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概 率;
率;
(Ⅱ)在这项考试过程中,假设他不放 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为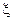 ,求
,求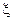 的数学期望E
的数学期望E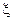 .
.