如图,点C在线段AB上,AC ="16" cm,CB ="12" cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB =" a" cm,其它条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在线段AB的延长线上,且满足AC BC =" b" cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由。
BC =" b" cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由。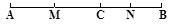
解方程: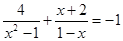
分解因式:(1) ;(2)
;(2)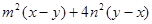
【问题提出】
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
【初步思考】
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
【深入探究】
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;
Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;
Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图,.
求证:.
证明: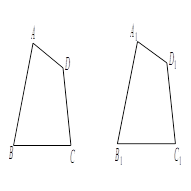
(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形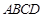 和四边形
和四边形 为例,分为以下四类:
为例,分为以下四类:
①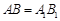 ,
,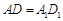 ,
,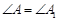 ,
,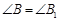 ,
,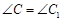 ;
;
②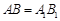 ,
,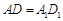 ,
,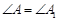 ,
,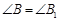 ,
,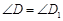 ;
;
③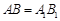 ,
,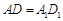 ,
,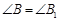 ,
,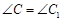 ,
,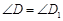 ;
;
④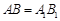 ,
,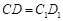 ,
,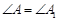 ,
,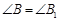 ,
,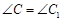 ;
;
其中能判定四边形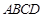 和四边形
和四边形 全等的是(填序号),概括可得“全等四边形的判定方法”,这个判定方法是.
全等的是(填序号),概括可得“全等四边形的判定方法”,这个判定方法是.
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨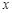 元(
元(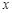 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为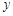 元.
元.
(1)求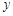 与
与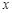 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量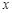 的取值范围;
的取值范围;
(2)若每个月的利润为2200元,求每件商品的售价应定为多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少元?
已知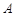 、
、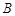 、
、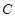 三点均在
三点均在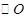 上,且
上,且 是等边三角形.
是等边三角形.
(1)如图,用直尺和圆规作出 ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
(2)若点 是
是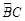 上一点,连接
上一点,连接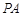 、
、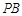 、
、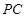 .探究
.探究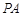 、
、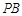 、
、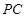 之间的等量关系并说明理由.
之间的等量关系并说明理由.