(12分)如图11所示,长L=1.2 m、质量M=3 kg的木板静止放在倾角为37°的光滑斜面上,质量m=1 kg、带电荷量q=+2.5×10-4 C的物块放在木板的上端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向垂直斜面向下、场强E=4.0×104 N/C的匀强电场.现对木板施加一平行于斜面向上的拉力F=10.8 N. 取g=10 m/s2,斜面足够长.求:
(1)物块经多长时间离开木板?
(2)物块离开木板时木板获得的动能.
(3)物块在木板上运动的过程中,由于摩擦而产生的内能.
一束初速度不计的电子在经U的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离d,板长 ,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间。已知电子质量为m,电荷量为e,求:
,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间。已知电子质量为m,电荷量为e,求:
(1)电子离开加速电场是的速度大小;
(2)电子经过偏转电场的时间;
(3)要使电子能从平行板间飞出,两个极板上最多能加多大电压?
(4)电子最远能够打到离荧光屏上中心O点多远处?
如图,水平匀强电场的电场强度为E,一个带电小球质量为m,轻质的绝缘细线长为L,静止时小球位于A点,细线与竖直方向成37°角,重力加速度为g,(sin370=0.6;cos370=0.8)求: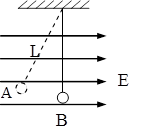
(1)小球带何种电荷?电荷量多少?
(2)现将小球拉回到竖直方向(图中B点),后由静止释放,小球通过A点位置时的速度大小是多少?
(3)若将小球到水平方向(图中C点)由静止释放,则小球通过A点位置时细线对小球的拉力为多大?
如图甲,在水平地面上固定一倾角为θ的光滑斜面,一劲度系数为k的轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态。一质量为m的滑块从距离弹簧上端为s0处静止释放,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g。
(1)求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1 (2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;
(2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;
(3)从滑块静止释放瞬间开始计时,请在乙图中画出滑块在沿斜面向下运动的整个过程中速度与时间关系v-t图象。图中横坐标轴上的t1、t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻,纵坐标轴上的v1为滑块在t1时刻的速度大小,vm是题中所指的物理量。(本小题不要求写出计算过程)
(12分)如图所示,光滑曲面的下端有一水平传送带,传送带正以4 m/s的速度运动,运动方向如图所示.一个质量为2 kg的物体(物体可以视为质点),从h="1.8" m高处由静止沿曲面下滑,物体与传送带间的动摩擦因数μ=0.2,若传送带足够长,取g="10" m/s²。试求: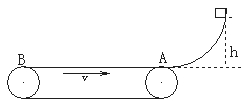
(1)物体由静止开始下滑到A处的速度?
(2)物体从A处向左运动的最大位移?
(3)物体从A处向左运动到最大位移处的过程中,物体与传送带组成的系统产生的摩擦热为多少?
(4)物体随传送带向右运动,最后沿斜面上滑的最大高度h′为多少?
(8分)如图所示,木块的质量m =" 2" kg,与地面间的动摩擦因数μ= 0.5,木块在拉力F="10" N作用下,在水平地面上从静止开始向右运动,运动2 m后撤去外力F。已知力F与水平方向的夹角θ= 37°,sin37°=0.6,cos37°=0.8,g取10m/s2。求: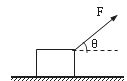
(1)刚撤去外力时,木块运动的速度;
(2)撤去外力后,木块还能滑行的距离为多少?