(本小题满分12分)
如图椭圆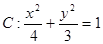 的右顶点是
的右顶点是 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形 是矩形(
是矩形(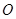 为原点),点
为原点),点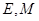 分别为线段
分别为线段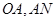 的中点.
的中点.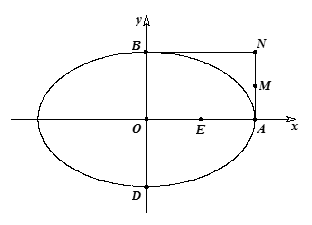
(Ⅰ)证明:直线 与直线
与直线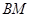 的交点在椭圆
的交点在椭圆 上;
上;
(Ⅱ)若过点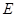 的直线交椭圆于
的直线交椭圆于 两点,
两点,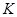 为
为 关于
关于 轴的对称点(
轴的对称点(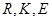 不共线),
不共线),
问:直线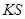 是否经过
是否经过 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
设曲线 在点A(x,
在点A(x, )处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x
)处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x k (x)
k (x)
 恒成立(
恒成立( ≠0).
≠0).
(1) 求 (1)的值;
(1)的值;
(2) 求函数k(x)的表达式;
(3) 求证: >
>
已知 是函数
是函数 的一个极值点。
的一个极值点。
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。
现有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,将这五个球放入5个盒子内.
(1)若只有一个盒子空着,共有多少种投放方法?
(2)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)若每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
已知 满足:
满足: ,
,
(1)求 ;
;
(2)猜想 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论
二项式 (
( 为大于零的常数)的展开式中各项的二项式系数之和为1024,按
为大于零的常数)的展开式中各项的二项式系数之和为1024,按 的升幂排列的前三项的系数之和是201.
的升幂排列的前三项的系数之和是201.
(1)求常数 和
和 ;
;
(2)求该二项展开式中含 项的系数.
项的系数.