有足够多的长方形和正方形卡片如下图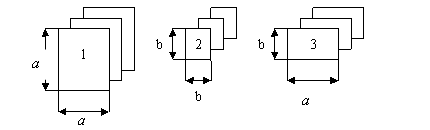
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.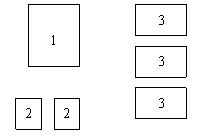
这个长方形的代数意义是
(2)小明想用类似方法解释多项式乘法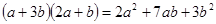
那么需用2号卡片 张,3号号卡片 张
某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜 元,且用 购买的甲种类型的数量与用 元购买的乙种类型的数量一样.
(1)求甲乙两种类型笔记本的单价.
(2)该学校打算购买甲乙两种类型笔记本共 件,且购买的乙的数量不超过甲的 倍,则购买的最低费用是多少.
某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.

(1)本次抽查总人数为______,“合格”人数的百分比为______;
(2)补全条形统计图;
(3)扇形统计图中“不合格人数”的度数为______;
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为______.
化简求值: ,其中 .
.
综合与实践
【问题情境】
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.
