如图，已知正比例函数和反比例函数的图象都经过点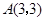
。
（1）求正比例函数和反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点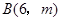
，求
的值和这个一次函数的解析式；
（3）第（2）问中的一次函数的图象与
轴、
轴分别交于C、D，求过A、B、D三点的二次函数的解析式；
（4）在第（3）问的条件下，二次函数的图象上是否存在点E，使
的面积
与
的面积S满足：
？若存在，求点E的坐标；若不存在，请说明理由。
解方程：（1）x2－4x＋2＝0；（2）2(x－3)＝3x(x－3)．
计算：（1）(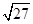
－
＋
)×
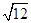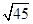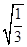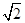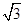；（2）(
－
)2＋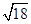
÷．
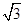如图是二次函数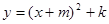
的图象，其顶点坐标为M(1,-4).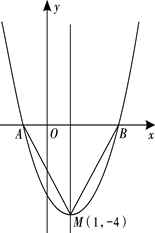
（1）求出图象与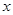
轴的交点A,B的坐标；
（2）在二次函数的图象上是否存在点P，使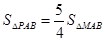
,若存在，求出P点的坐标；若不存在，请说明理由；
（3）将二次函数的图象在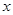轴下方的部分沿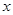轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线
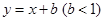与此图象有两个公共点时，
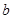的取值范围.
如图，抛物线形的拱桥在正常水位时，水面AB的宽为20m.涨水时水面上升了3m，达到了警戒水位，这时水面宽CD＝10m.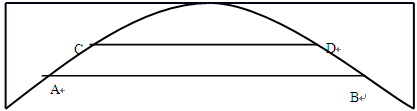
（1）求抛物线的解析式；
（2）当水位继续以每小时0.2m的速度上升时，再经过几小时就到达拱顶？
如图，已知抛物线C1：
的顶点为P， 与x轴相交于A、B两点（点A在点B的左侧），点B 的横坐标是1．
（1）求a的值；
（2）如图，抛物线C2与抛物线C1关于x轴对称，将抛物 线C2向右平移，平移后的抛物线记为C3，抛物线
C3的顶点为M，当点P、M关于点O成中心对称时，求抛物线C3的解析式．