如图,已知抛物线C1: 的顶点为P, 与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.
的顶点为P, 与x轴相交于A、B两点(点A在点B的左侧),点B 的横坐标是1.
(1)求a的值;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物 线C2向右平移,平移后的抛物线记为C3,抛物线
C3 的顶点为M,当点P、M关于点O成中心对称时,求抛物线C3的解析式.
九年级(1)班要举行一场毕业联欢会,规定每个同学同时转动下图中①、②两个转盘(两个转盘分别被二等分和三等分),若两个转盘停止后指针所指的数字之和为奇数,则这个同学要表演唱歌节目;若数字之和为偶数,则要表演其他节目.试求出这个同学表演唱歌节目的概率(要求用画树状图或列表方法求解).
反比例函数 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
下图是一个立体图形的三视图,请根据视图写出该立体图形的名称,并计算该立体图形的体积(结果保留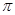 ).
).
(本题9分)如图,对称轴为x= 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式;
(2)设点E( ,
, )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
某农场要建一个长方形ABCD的养鸡场,鸡场的一边靠墙,(墙长25m)另外
三边用木栏围成,木栏长40m。
(1)若养鸡场面积为168m2,求鸡场的一边AB的长。
(2)请问应怎样围才能使养鸡场面积最大?最大的面积是多少?
(3)养鸡场面积能达到205m2吗?如果能,请给出设计方案,如果不能,请说明理由。