(本题9分)如图,对称轴为x= 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式;
(2)设点E( ,
, )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.
(1)如图1,当OA=OB且D为AO中点时,求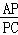 的值;
的值;
(2)如图2,当OA=OB, 时,求tan∠BPC.
时,求tan∠BPC.
随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2009年底拥有家庭电动自行车125辆,2011年底家庭电动自行车的拥有量达到180辆.
(1)若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2012年底电动自行车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
先化简,再求值:(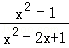 +
+ )÷
)÷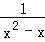 ,其中x满足x2+x﹣2=0.
,其中x满足x2+x﹣2=0.
已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.