在四边形
中，对角线AC与BD交于点O，△ABO≌△CDO.
求证：四边形
为平行四边形若∠ABO=∠DCO，求证：四边形
为矩形.
解不等式组或方程求不等式组
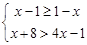的整数解解分式方程
．
计算
化简：
如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点， HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．求证：△DHQ∽△ABC
求y关于x的函数解析式并求y的最大值
当x为何值时，△HDE为等腰三角形？
如图，在平面直角坐标系中放置一矩形ABCO，其顶点为A（0，1）、B（－3，1）、C（－3，0）、O（0，0）．将此矩形沿着过E（－，1）、
F（－，0）的直线EF向右下方翻折，B、C的对应点分别为B′、C′求折痕所在直线EF的解析式
一抛物线经过B、E、B′三点，求此二次函数解析式；
能否在直线EF上求一点P，使得△PBC周长最小？如能，求出点P的坐标；若不能，说明理由．
+
）÷
，其中x满足x2+x﹣2=0．