平面内两条直线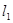 ∥
∥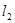 ,它们之间的距离等于a,一块正方形纸板
,它们之间的距离等于a,一块正方形纸板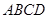 的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.
的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.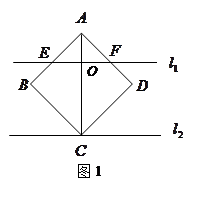
(1)如图1,将点C放置在直线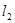 上,且
上,且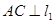 于O,使得直线
于O,使得直线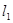 与
与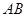 、
、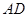 相交于E、F.求证:①BE="OE" ②
相交于E、F.求证:①BE="OE" ②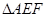 的周长等于
的周长等于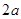 ;
;
(2)如图2,若绕点C转动正方形硬纸板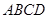 ,使得直线
,使得直线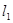 与
与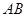 、
、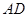 相交于E、F,试问
相交于E、F,试问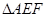 的周长等于
的周长等于 还成立吗?并证明你的结论;
还成立吗?并证明你的结论;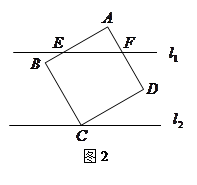
(3)如图3,将正方形硬纸片 任意放置,使得直线
任意放置,使得直线 与
与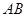 、
、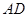 相交于E、F,直线
相交于E、F,直线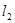 与
与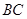 、CD相交于G,H,设
、CD相交于G,H,设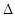 AEF的周长为
AEF的周长为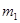 ,
,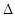 CGH的周长为
CGH的周长为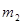 ,试问
,试问
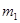 ,
,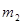 和
和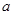 之间存在着什么关系?试直接写出你的结论(不需证明).
之间存在着什么关系?试直接写出你的结论(不需证明).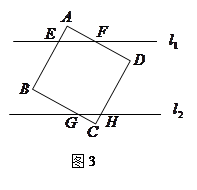
⑴ 在图①中,用阴影画出图形1沿图中虚线翻折后的图形。
⑵ 在图②中,用阴影画出图形1绕图中的空心点旋转180°后的图形。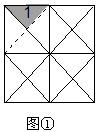

解方程:(每题5分,共10分)
(1) (2)
(2) 
如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.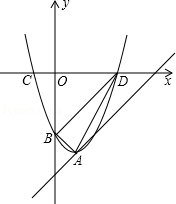
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C.D(C点在D点的左侧),试判断△ABD的形状;
(3)是否存在一点P,使以点P、A.B.D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心, PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax²+bx+4过A,B,C三点且AB=6.
⑴求⊙P的半径R的长;
⑵若点E在y轴上,且△ACE是等腰三角形,试写出所有点E的坐标;