.(满分12分)某射击比赛,开始时在距目标100米处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150米处,这时命中记2分,且停止射击;若第二次仍未命中还可以进行第三次射击,但此时目标已在200米处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分。已知射手在100米处击中目标的概率为 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
(1)求这名射手在射击比赛中命中目标的概率;
(2)求这名射手在比赛中得分的数学期望。
已知函数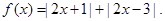
(1)求不等式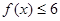 的解集;
的解集;
(2)若关于x的不等式 的解集非空,求实数
的解集非空,求实数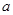 的取值范围.
的取值范围.
如图,已知四边形ABCD内接于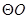 ,且AB是的
,且AB是的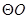 直径,过点D的
直径,过点D的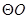 的切线与BA的延长线交于点M.
的切线与BA的延长线交于点M.
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小.
已知函数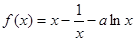
(1)若函数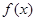 在点
在点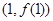 处的切线与圆
处的切线与圆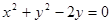 相切,求
相切,求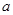 的值;
的值;
(2)当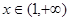 时,函数
时,函数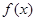 的图像恒在坐标轴
的图像恒在坐标轴 轴的上方,试求出
轴的上方,试求出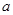 的取值范围.
的取值范围.
已知函数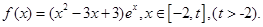
(1)当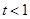 时,求函数
时,求函数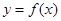 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间. ,试问函数
,试问函数 在
在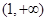 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知 为锐角,且
为锐角,且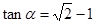 ,函数
,函数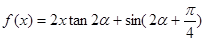 ,数列{
,数列{ }的首项
}的首项 .
.
(1)求函数 的表达式;
的表达式;
(2)求数列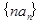 的前
的前 项和
项和 .
.