为了加快经济的发展,某省选择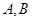 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在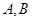 两城市的周边修建城际轻轨,假设
两城市的周边修建城际轻轨,假设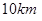 为一个单位距离,
为一个单位距离,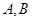 两城市相距
两城市相距 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为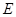 ,使轻轨
,使轻轨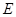 上的点到
上的点到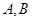 两城市的距离之和为
两城市的距离之和为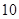 个单位距离,
个单位距离,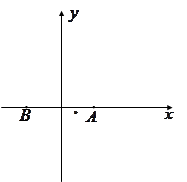
(1)建立如图的直角坐标系,求城际轻轨所在曲线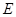 的方程;
的方程;
(2)若要在曲线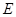 上建一个加油站
上建一个加油站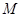 与一个收费站
与一个收费站 ,使
,使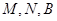 三点在一条直线上,并且
三点在一条直线上,并且 个单位距离,求
个单位距离,求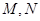 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?
(3)在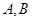 两城市之间有一条与
两城市之间有一条与 所在直线成
所在直线成 的笔直公路
的笔直公路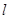 ,直线
,直线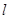 与曲线
与曲线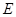 交于
交于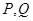 两点,求四边形
两点,求四边形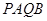 的面积的最大值.
的面积的最大值.