如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=
,BC= 1,PA=2,E为PD的中点.
1,PA=2,E为PD的中点.
(1)求直线AC与PB所 成角的余弦值;
成角的余弦值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点 到AB和AP的距离.
到AB和AP的距离.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.
⑴求异面直线PD与AE所成角的大小;
⑵求证:EF⊥平面PBC ;
⑶求二面角F—PC—B的大小.
(本小题满分12分)
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3. 设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲、乙两种保险中的一种的概率;
(2)求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
(本小题满分12分)
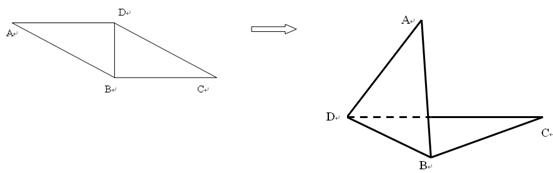
在四边形ABCD中,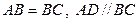 ,且
,且 ,沿
,沿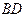 将其折成一个二面角
将其折成一个二面角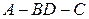 ,使
,使 .
.
(1)求折后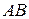 与平面
与平面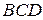 所成的角的余弦值;
所成的角的余弦值;
(2)求折后点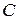 到平面
到平面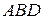 的距离.
的距离.
(本小题满分12分)
已知函数 在
在 处有极小值
处有极小值 .
.
(1)求函数 的单调区间;
的单调区间;
(2)求函数 在闭区间
在闭区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分10分)
设等比数列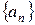 的前
的前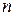 项和为
项和为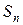 .已知
.已知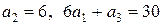 ,求
,求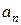 和
和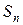 .
.