(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.
⑴求异面直线PD与AE所成角的大小;
⑵求证:EF⊥平面PBC ;
⑶求二面角F—PC—B的大小.
已知抛物线 的焦点为F,平行于x轴的两条直线 , 分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明 ;
(2)若 的面积是 的面积的两倍,求AB中点的轨迹方程.
如图,四棱锥 中, , , , ,M为线段AD上一点, ,N为PC的中点.

(1)证明 ;
(2)求四面体 的体积.
如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
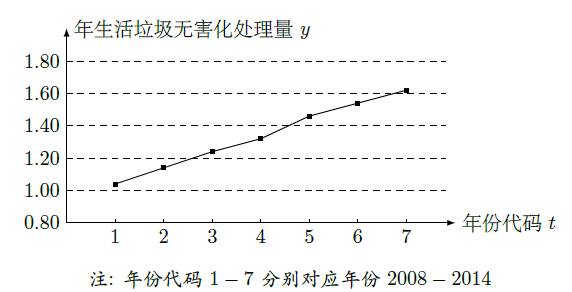
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .
已知各项都为正数的数列 满足 ,
(1)求 , ;
(2)求 的通项公式.
设定义在R上的函数 满足:对于任意的x 1、x 2∈R,当 时,都有 .
(1)若 ,求a的取值范围;
(2)若 是周期函数,证明: 是常值函数;
(3)设 恒大于零, 是定义在R上的、恒大于零的周期函数,M是 的最大值.函数 .证明:" 是周期函数"的充要条件是" 是常值函数".