（本小题满分12分）
根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3. 设各车主购买保险相互独立.
（1）求该地1位车主至少购买甲、乙两种保险中的一种的概率；
（2）求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
在直角坐标系xOy中，圆C的参数方程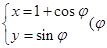
为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（Ⅰ）求圈C的极坐标方程；
（Ⅱ）直线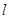
的极坐标方程是
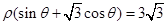，射线
与圆C的交点为O,P与直线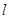的交点为Q，求线段PQ的长．
如图，在直线三棱柱ABC—A1B1C1中，AB=AC=1，∠BAC=90°，异面直线A1B与B1C1所成的角为60°．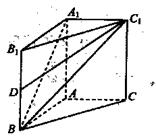
（Ⅰ）求证：AC⊥A1B；
（Ⅱ）设D是BB1的中点，求DC1与平面A1BC1所成角的正弦值．
设数列{an}是等差数列，数列{bn}的前n项和Sn满足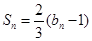
且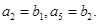
（Ⅰ）求数列{an}和{bn}的通项公式：
（Ⅱ）设Tn为数列{Sn}的前n项和，求Tn．
已知数列
的前
项和
（为正整数）。
（1） 令
，求证：数列
是等差数列，并求数列的通项公式；
（2） 令
，
，求使得
成立的最小正整数，并证明你的结论.
在△
中，角A,B,C的对边分别为
，且
（1）求角B的大小；
（2）若
且
，求
的取值范围.