腾蛟人本超市欲招聘收银员一名,对A、B、C三名候选人进行了三项素质测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如表所示: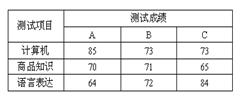
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用,说明理由;
(2)人本集团根据实际需要,将计算机、商品知识和语言表达能力测试得分按5:3:2的比例确定每人的成绩,此时谁将被录用?请写出推理过程。
方程:

解方程: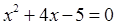
如图1,在平面直角坐标系xoy中,Rt△AOB的斜边OB在x轴上,其中∠ABO=30°,OB=4。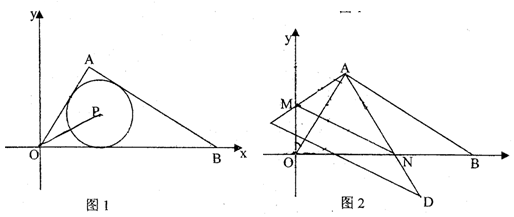
⑴直接写出,Rt△AOB的内心和P的坐标;
⑵如图2,若将Rt△AOB绕其直角顶点A顺时针旋转α度(0°<α<90°),得到
 Rt△ACD,直角边AD与x轴相交于点N,直角边AC与y轴相交于点M,连结MN。设△MON的面积为S△MON,△AOB的面积为S△AOB,以点M为圆心,MO为半径作⊙M,
Rt△ACD,直角边AD与x轴相交于点N,直角边AC与y轴相交于点M,连结MN。设△MON的面积为S△MON,△AOB的面积为S△AOB,以点M为圆心,MO为半径作⊙M,
①当直线AD与⊙M相切时,试探求S△MON与S△AOB之间的 关系。
关系。
②当S△MON =
=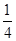 S△AOB时,试判断直线A
S△AOB时,试判断直线A D与⊙M的位置关系,并说明理由。
D与⊙M的位置关系,并说明理由。
已知:正方形ABCD的边长为4,⊙O交正方形ABCD的对角线AC所在直线于点T,连接TO交⊙O于点S。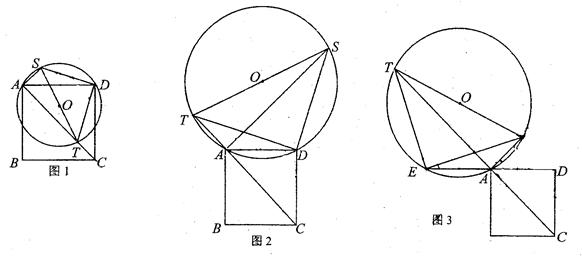
⑴如图1,当⊙O经过A、D两点且圆心O在正方形ABCD内部时,连结DT、DS。
①试判断线段DT、DS的数量关系和位置关系;②求AS+AT的值;⑵如图2,当⊙O经过A、D两点且圆心O在正方形ABCD外部时,连结DT、DS。
求AS—AT的值。⑶如图3,延长DA到点E,使AE=AD,当⊙O经过A、E两点时,连结ET、ES。根据⑴、⑵计算,通过观察、分析,对线段AS、AT的数量关系提出问题并解答。
某学校计划利用一片空地建一个学生自行车车棚,自行车车棚为矩形,其中一面靠墙,这堵墙的长度为12米,另二面墙用现有的木板材料围成 ,总长为26米,且计划建造车棚的面积为80平方米。
,总长为26米,且计划建造车棚的面积为80平方米。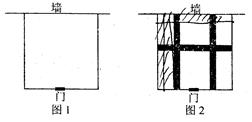
⑴如图1,为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
⑵如图2,为了方便学生取车,施工单位又决定在车棚内修建三条等宽的小路(小路垂直或平行于墙),使得停放自行车的面积为54平方米,那么小路的宽度是多少米?