如图，在等腰梯形ABCD中，AD∥BC，ABDC5，AD6，-优题课

如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12，动点P从A点出发以每秒1个单位的速度向终点D运动，动点Q从C点出发以每秒2个单位的速度向终点B运动，两点同时出发，设运动时间为t.
（1）梯形ABCD的面积是。
（2）①当t为多少秒时，四边形ABQP是平行四边形？
②当t为多少秒时，四边形ABQP是梯形？
（3）当t=3秒时通过计算判断四边形ABQP是否是直角梯形？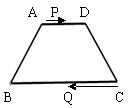

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

定义:如果一元二次方程 $a x^{2} + bx + c = 0 (a \neq 0)$ 满足 $a + b + c = 0$ ，那么我们称这个方程为“凤凰方程”，已知 $a x^{2} + bx + c = 0 (a \neq 0)$ 是“凤凰方程”，且有两个相等的实数根，求 $a, b, c$ 之间的关系.

已知关于 $x$ 的一元二次方程 $x^{2} - (2 k + 1) x + k^{2} + k = 0$ .

（1）求证:无论 $k$ 取何值，方程都有两个不相等的实数根.

（2）如果方程的两个实数根为 $x_{1}, x_{2}$ ，且 $k$ 与 $\frac{x_{1}}{x_{2}}$ 都为整数，求 $k$ 所有可能的值.

设 $m$ 是不小于 $- 1$ 的实数，关于 $x$ 的方程 $x^{2} + 2 (m - 2) x + m^{2} - 3 m + 3 = 0$ 有两个不相等的实数根 $x_{1}, x_{2}$ .

（1）若 $x_{1}^{2} + x_{2}^{2} = 6$ ，求 $m$ 的值；

（2）求 $\frac{m x_{1}^{2}}{1 - x_{1}} + \frac{m x_{2}^{2}}{1 - x_{2}}$ 的最大值.

已知关于 $x$ 的方程 $x^{2} - (2 k - 1) x + k^{2} = 0$ 有两个实根 $x_{1}, x_{2}$ ，且满足 $x_{1} x_{2} - |x_{1}| - |x_{2}| = 2$ ，求实数 $k$ 的值；

如图，在 $▱ A B C D$ 中， $P$ 是线段 $B C$ 中点，联结 $B D$ 交 $A P$ 于点 $E$ ，联结 $C E$ ．

（1）如果 $A E ＝ C E$ ．

ⅰ．求证： $▱ A B C D$ 为菱形；

ⅱ．若 $A B ＝ 5 ， C E ＝ 3$ ，求线段 $B D$ 的长；

（2）分别以 $A E ， B E$ 为半径，点 $A ， B$ 为圆心作圆，两圆交于点 $E ， F$ ，点 $F$ 恰好在射线 $C E$ 上，如果 $C E = \sqrt{2} A E$ ，求 $\frac{AB}{BC}$ 的值．

试卷网试题网古诗词网作文网范文网