短跑名将博尔特在北京奥运会上创造了100 m和200 m短跑项目的新世界纪录,他的成绩分别是9.69 s和19.30 s.假定他在100 m比赛时从发令到起跑的反应时间是0.15 s,起跑后做匀加速运动,达到最大速率后做匀速运动.200 m比赛时,反应时间及起跑后加速阶段的加速度和加速时间与100 m比赛时相同,但由于弯道和体力等因素的影响,以后的平均速率只有跑100 m时最大速率的96%.求:
(1)加速所用时间和达到的最大速率;
(2)起跑后做匀加速运动的加速度.(结果保留两位小数)
如图所示,空间区域I、II有匀强电场和匀强磁场,MN、PQ为理想边界,I区域高度为d,II区域的高度足够大,匀强电场方向竖直向上;I、II区域的磁感应强度大小均为B,方向分别垂直纸面向里和向外。一个质量为m、带电荷量为q的小球从磁场上方的O点由静止开始下落,进入场区后,恰能做匀速圆周运动。已知重力加速度为g。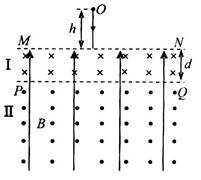
(1)试判断小球的电性并求出电场强度E的大小;
(2)若带电小球运动一定时间后恰能回到O点,求它释放时距MN的高度h;
(3)试讨论在h取不同值时,带电小球第一次穿出I区域的过程中,电场力所做的功。
工厂里有一种运货的过程可以简化为如图所示,货物以 的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数
的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数 ,货物可简化为质点,斜面的倾角为
,货物可简化为质点,斜面的倾角为 。
。
(1)求货物从A点到B点的时间;
(2)求AB之间的水平距离;
(3)若已知OA段距离足够长,导致货物在碰到A之前已经与货车达到共同速度,则货车的长度是多少?
如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为L=1m,质量m=0.1kg的导体棒,ab导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面。当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程中导体棒产生热量Q=2J。电动机工作时,电压表、电流表的读数分别为U=7V和I=1A,电动机的内阻r=1Ω。不计一切摩擦,g取10m/s2。求: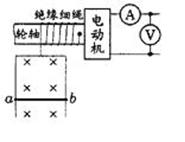
(1)导体棒所达到的稳定速度是多少?
(2)导体棒从静止到达稳定速度的时间是多少?(本题20分)
某小水电站发电机输出的电功率为P="100" kW,输出电压为U1="250" V.现准备向远处输电,所用输电线的总电阻为R=8Ω,要求在输电线上的损失电功率为输出的电功率的5%,用户获得U4="220" V电压,求所选用的升压变压器原、副线圈的匝数比和降压变压器原、副线圈的匝数比.(本题17分)
如图所示,单摆摆长为Lm,做简谐运动,C点在悬点O的正下方,D点与C相距为X m,C、D之间是光滑水平面,当摆球A到左侧最大位移处时,小球B从D点以某一速度v匀速地向C点运动,A、B二球在C点迎面相遇,求小球B的速度大小。 (重力加速度为g)(本题15分)