如图所示，空间区域I、II有匀强电场和匀强磁场，MN、PQ为理想边界，I区域高度为d，II区域的高度足够大，匀强电场方向竖直向上；I、II区域的磁感应强度大小均为B，方向分别垂直纸面向里和向外。一个质量为m、带电荷量为q的小球从磁场上方的O点由静止开始下落，进入场区后，恰能做匀速圆周运动。已知重力加速度为g。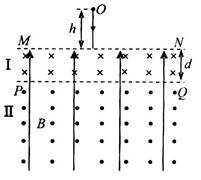
（1）试判断小球的电性并求出电场强度E的大小；
（2）若带电小球运动一定时间后恰能回到O点，求它释放时距MN的高度h；
（3）试讨论在h取不同值时，带电小球第一次穿出I区域的过程中，电场力所做的功。
发电机输出功率为100 kW，输出电压是250 V，用户需要的电压是220 V，输电线电阻为10 Ω.若输电线中因发热而损失的功率为输送功率的4%。
如图所示的电路中，电源电动势E =" 6.0V" ，内阻r =" 0.6Ω" ，电阻R2 =" 0.5Ω" ，当开关S断开时，电流表的示数为1.5A，电压表的示数为3.0V ，试求：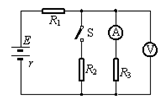
电阻R1和R3的阻值
当S闭合后，求电压表的示数和R2上消耗的电功率
如图，光滑的圆槽固定不动，处于水平向里的匀强磁场中，一带正电小球从与圆心等高处由静止沿圆槽下滑，到达最低点。已知小球质量m=0.1g，电量q=1.0×10-6C圆槽半径 R=1.25m，磁感应强度B=2×102T(g=10m/s2)
求: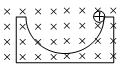
小球运动到最低点时的速度大小？
小球在最低点圆槽对小球的支持力？
如图所示,位于竖直平面上的1/4圆弧轨道AB光滑无摩擦,轨道半径为R，O点为圆心,A点距地面高度为H.质量为m的小球从A点由静止释放,通过B点时对轨道的压力为3mg,最后落在地面C处.不计空气阻力,求: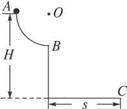
小球通过B点的速度;
小球落地点C与B点的水平距离s;
比值
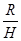为多少时,C与B点的水平距离s最大，最大值是多少?
在冬天，高为h＝1.25m的平台上，覆盖一层薄冰，一乘雪橇的滑雪爱好者，从距平台边缘s＝24m处以一定的初速度向平台边缘滑去，如图所示，当他滑离平台即将着地时的瞬间，其速度方向与水平地面的夹角为 θ＝45°，取重力加速度g＝10m/s2。滑雪者着地点到平台边缘的水平距离是多大；
若平台上的薄冰面与雪橇间的动摩擦因数为μ＝0.05，则滑雪者的初速度是多大？