已知⊙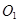 、⊙
、⊙ 外切于点
外切于点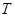 ,经过点
,经过点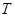 的任一直线分别与⊙
的任一直线分别与⊙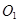 、⊙
、⊙ 交于点
交于点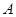 、
、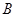 ,
,
(1)若⊙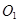 、⊙
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证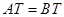 ;
;
(2)若⊙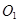 、⊙
、⊙ 的半径分别为
的半径分别为 、
、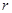 (如图2),试写出线段
(如图2),试写出线段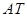 、
、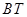 与
与 、
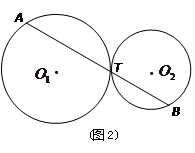
、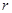 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).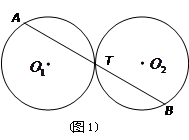
甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
六·一”儿童节前夕,某童装专卖店用2500元购进一批儿童服装,上市后很快脱销,接着又用4500元购进第二批这种服装,所购数量是第一批数量的1.5倍,但每套进价多了10元.
(1)求第一批童装每套的进价是多少元?
(2)如果这两批童装每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数) 
如图,方格纸中的每个小正方形边长都是1个单位长度,Rt△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A1B2C2,试在图中画出Rt△A1B2C2,并计算Rt△A1B1C1在上述旋转过程点C1所经过的路径长.
先化简,再求值: ,其中a= -1
,其中a= -1